Cu siguranță, cu toții am auzit de teoria probabilității, chiar dacă nu o avem foarte bine definită în minte. Ei bine, aflați că o folosiți mult mai des decât vă puteți imagina, în lucruri banale zilnice. Ce este aceasta și cine a descoperit-o?
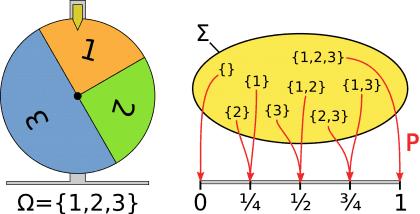
Pentru început, să vedem ce este teoria probabilității. Într-o descriere simplă, putem defini această ramură a matematicii ca raportul dintre numărul situațiilor favorabile pentru ca un anumit eveniment să se petreacă și numărul tuturor situațiilor egal posibile. Mai exact, studiază legile după care evoluează fenomenele aleatorii. Probabilitatea este cuantificată ca un număr între zero și unu, unde zero reprezintă imposibilitatea ca acel lucru să se petreacă, iar unu reprezintă siguranța ca acel lucru să se întâmple. Bineînțeles, aceasta este varianta simplificată a teoriei. Dacă doriți să-i explicați cuiva despre această teorie, aflați că există o sumedenie de metode extrem de simple.
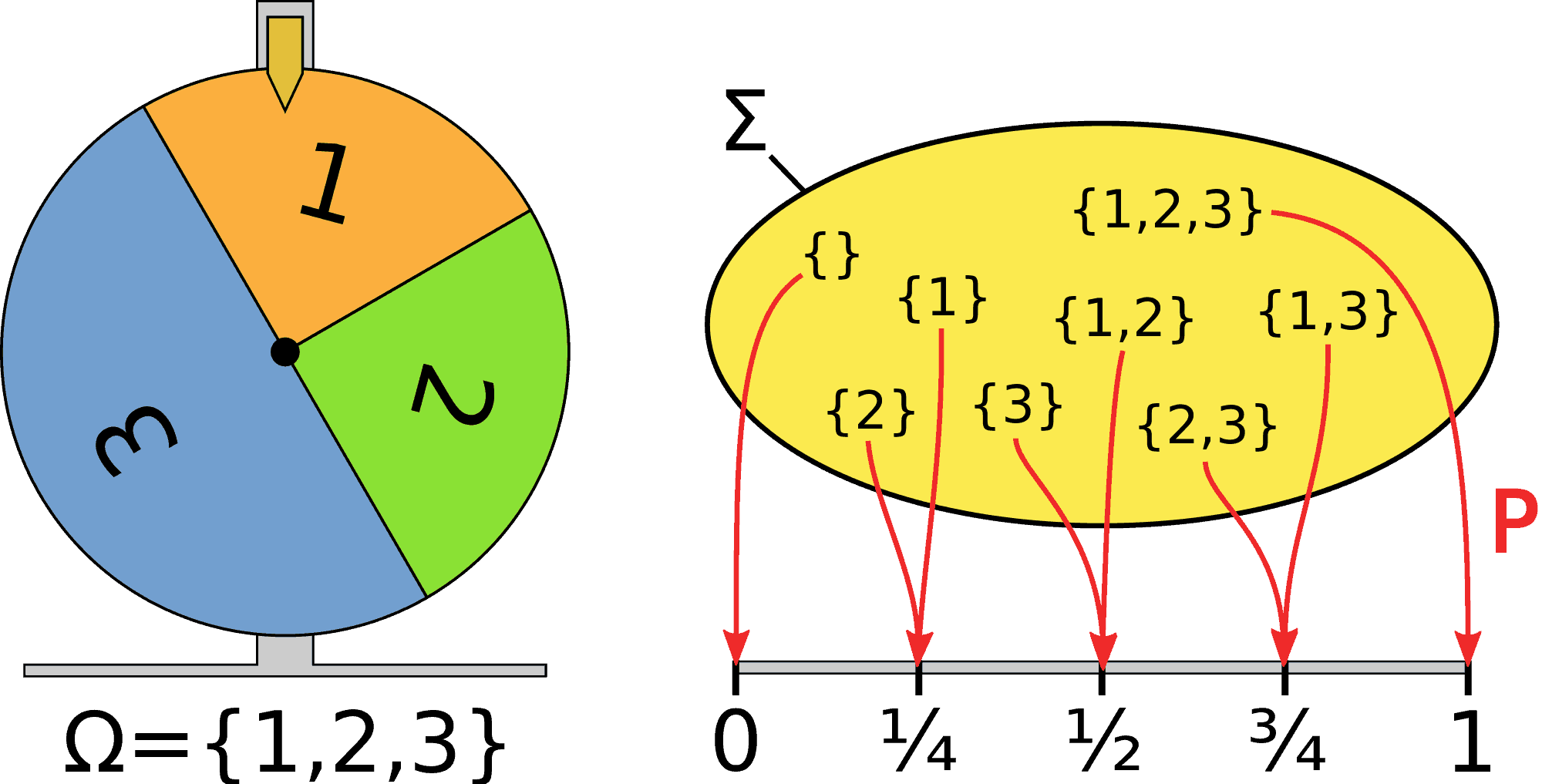
Foto: Pixabay
Aflăm pentru prima oară despre teoria probabilității în Franța, în secolul al XVII-lea, în corespodența dintre matematicianul Blaise Pascal – numele cel mai cunoscut legat de această teorie – și Pierre de Fermat, un avocat francez. Corespondenţa dintre cei doi a început ca rezultat al întrebărilor despre jocurile de noroc. Totuși, un alt nume ar trebui să aibă aceeași rezonanță ca a lui Pascal, atunci când se aduce în discuție teoria probabilității. Numele lui este Giralamo Cardano, un matematician și un scriitor prolific din Italia, născut în 1501. A abordat numeroase subiecte de-a lungul carierei sale, însă era și un jucător convins al jocurilor de noroc. Astfel, a scris Liber de Ludo Aleae (Cartea Jocurilor de Noroc ), operă ce a contribuit la teoria probabilității și înțelegerea șanselor. Din păcate, această scriere a fost descoperită la aproape un secol după moartea lui Cardano și a fost publicată în 1663.
Mai târziu, în secolul al XIX-lea, această ramură matematică a fost dezvoltată de Abraham Moivre, Pierre Simon Laplace și Carl Friedrich Gauss. În secolul al XX-lea, asociem numele lui Andrei Nikolaevici Kolmogorov și al lui Alexandr Iakovlevici Hincin de teoria probabilității.
În viața noastră, majoritatea evenimentelor ce se petrec pe termen scurt și pe termen lung sunt aleatorii. Așa a apărut și necesitatea de a studia o știință a hazardului. Așa că nu ar strica să aplicăm puțină matematică din când în când, astfel ne-am putea crește șansele de a cunoaște dinainte rezultatul final. Ca de exemplu, de câte ori nu ni s-a întâmplat ca un anumit eveniment să se petreacă într-un mod repetat – cum ar fi mersul la pâine, parcatul mașinii, mersul la cumpărături etc. – în condiții aproape identice? Ei bine, frecvența cu care apare un anumit rezultat – ca de exemplu, cumpăratul unei pâini albe doar, parcatul lateral reușit sau beneficierea de prețuri reduse – este aproximativ aceeași, oscilând în jurul unui număr constant. Acest număr pe care îl atribuim reprezintă probabiltatea ca acel final să se petreacă.

Foto: Wikipedia
Deși este un proces imposibil să prezici la perfecție finalul unor întâmplări aleatorii, ele pot fi analizate și procesate, iar elementele comune găsite te pot ajuta să-ți înțelegi șansele mai bine. Să luăm spre exemplu jocul de table sau orice alt joc în care se folosesc zaruri. În momentul în care vorbim depre zaruri sau chiar și despre jocuri de noroc, așa cum vorbeau Pascal și Ferrat, intervine negreșit termenul de probabilitate. Care este probabilitatea să îți pice dublă la jocul de table? Ei bine, având în vedere că sunt șase numere, șase duble posibile, iar numărul total de cazuri este de treizeci şi şase, aflăm că șanse foarte, foarte mari nu prea sunt. Împărțim șase la treizeci şi şase și avem ca rezultat 0,1667. Iată că probabilitatea este de doar 16,67%. Care sunt șansele de a ne pica un șase atunci, pe oricare dintre zaruri? Dacă vom calcula puțin, aflăm că posibilități sunt şaptesprezece, în combinație cu celelalte numere, iar totalul de cazuri rămâne tot treizeci şi şase. Șansa de a obține un șase este de 47,22%.
Același calcul simplu îl putem extrapola pe orice fel de activitate pe care o întreprindem și la care ne dorim să cunoaștem cât de cât finalul. Trebuie doar să știm numărul total al posibilităților, plus numărul situațiilor favorabile.
















Lasă un comentariu